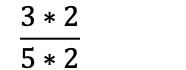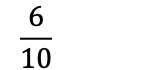Hva er en brøk?
En brøk er en måte å uttrykke en del av en helhet på. Den består av to hoveddeler:
- Teller: Tallet som står øverst og viser hvor mange deler vi har.
- Nevner: Tallet som står nederst og viser hvor mange like store deler helheten er delt opp i.
For eksempel, i brøken:

- 1 er telleren, som viser at vi har én del.
- 2 er nevneren, som viser at helheten er delt i to like store deler.
Eksempel
Si at vi har en pizza delt i 8 like store deler. Hvis du spiser 3 av disse delene, kan vi uttrykke det som en brøk.
- Teller: 3 (fordi du spiser 3 deler).
- Nevner: 8 (fordi pizzaen er delt i 8 deler).
Brøken som representerer hvor mye pizza du har spist blir:
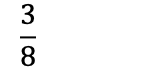
Dette betyr også at vi har igjen 5 pizzastykker. Det kan uttrykkes som:
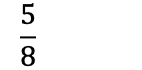
Addere brøk
La oss si vi skal løse følgende regnestykke:
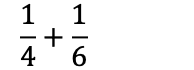
Å legge sammen brøker som ikke har felles nevner, kan ikke legges sammen direkte. Dette kan enklere forstås ved å illustrere brøkene som pizzastykker:
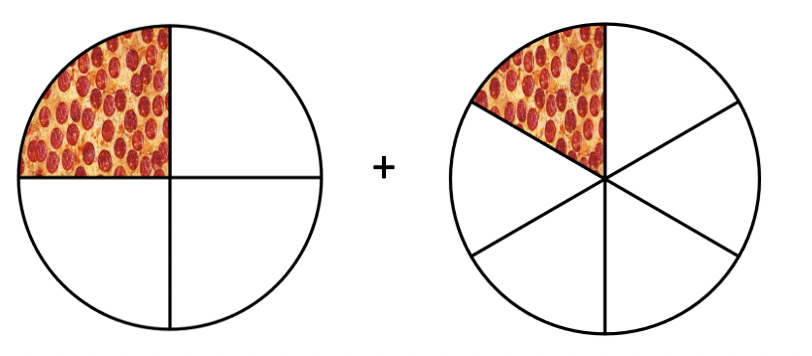
Om vi bare nå legger sammen antall pizzastykker, så får vi 2, men dette blir ikke helt riktig da de er av ulik størrelse. For å løse dette på riktig måte, vil vi derfor gjøre om slik at begge pizzaene er delt opp i like mange biter.
Om vi deler pizzaene opp i 12 biter, får vi dette:
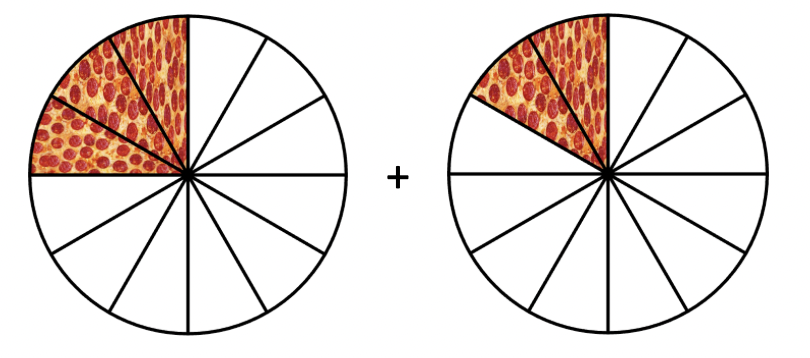
Når vi har like store biter, kan vi enkelt bare legge sammen antall biter. I dette tilfellet får vi dermed 3 + 2 = 5:
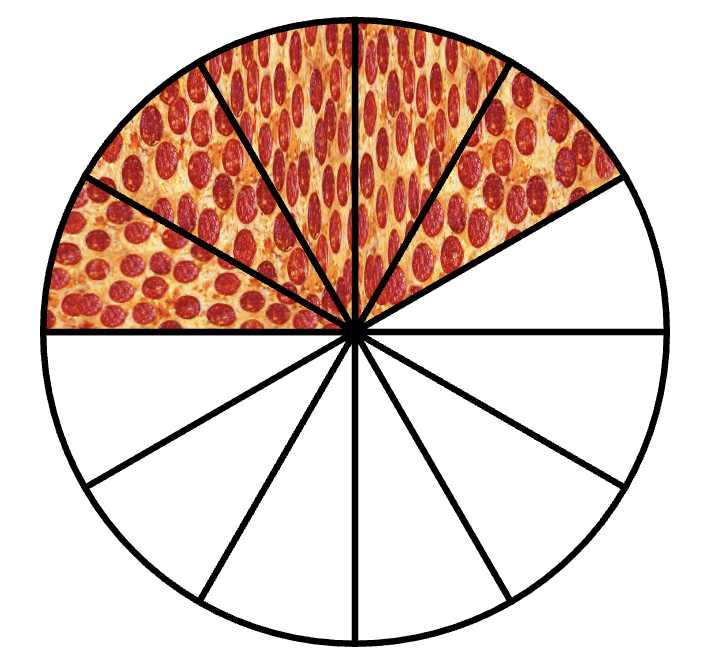
Gjør vi de to pizzaene om igjen til brøk, får vi:
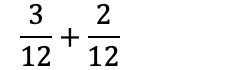
Nå som vi har to brøker med lik nevner, kan vi legge sammen tellerne:
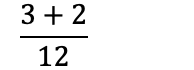
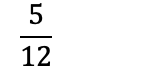
For å legge sammen brøker, er vi dermed avhengige av å finne en lik nevner – en fellesnevner
Eksempel
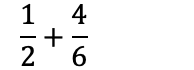
Vi har to brøker med ulik nevner, og må derfor starte med å finne fellesnevner.
Det gjøres ved å finne ut om det er et tall som begge nevnertallene har i sin gangetabell. Den enkelte måten å finne et slikt tall på, er å gange nevnerne med hverandre. Men om det finnes et fellestall som er lavere, vil vi som regel bruke det.
I dette tilfellet skal vi finnes fellesnevner med tallene 2 og 6. Den miste fellesnevneren her er 6, da 2×3 blir 6 og 6×1 blir 6.
I brøkene, ganger vi teller og nevner med tallene vi brukte for å skaffe fellesnevner:
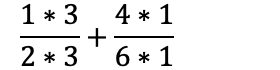
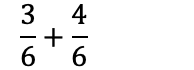
Nå som vi har lik nevner i begge brøker, kan man legge de sammen:
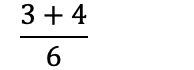
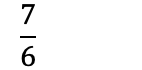
Subtrahere brøk
Når vi skal trekke fra med brøk, gjør vi det samme som ved addisjon.
Eksempel
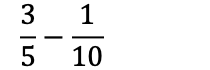
Finne fellesnevner: 5 og 10 har begge 10 i sin gangetabell. 5×2 = 10 og 10×1 = 10
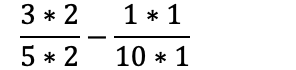
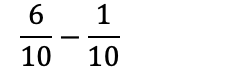
Med lik nevner løser vi brøkstykket:
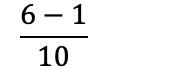
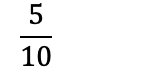
Multiplisere brøk
Når man multipliserer brøk, multipliserer man teller med teller, og nevner med nevner.
Eksempel
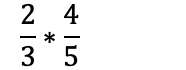
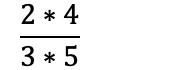
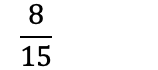
Dividere brøk
Når man dividerer brøk, multipliserer man den første brøken med den inverse av den andre brøken. Vi får invers brøk ved å bytte plass på teller og nevner.
Eksempel
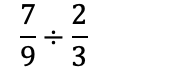
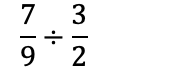
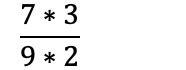
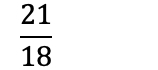
Når man regner med brøk, vil man som oftest ha så liten brøk som mulig. Vi forkorter derfor brøken ved å dele på samme tall over og under brøkstreken:
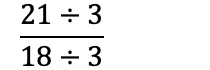
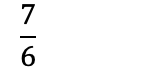
Å forkorte og å utvide brøk
Å forkorte eller å utvide en brøk vil si at vi gjør tallene i brøken mindre eller større. Dette kan vi for eksempel bruke for å gjøre en brøk enklere å regne med.
Å forandre på tallene i en brøk endrer ikke verdien til brøken så lenge man ganger eller deler med det samme tallet
Å forkorte brøk
Når vi forkorter en brøk, deler vi teller og nevner på det samme tallet, noe som gjør at brøken består av lavere tall, og blir lettere å jobbe med:
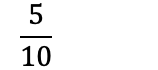
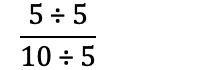
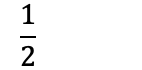
Det betyr også at 5/10 er det samme som 1/2:
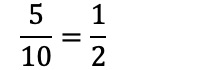
Noen ganger kan det være vanskelig å finne ut hvilket tall man burde dele på for å få lavest mulig brøk. Løsningen er å først sjekke om teller og nevner er partall. Hvis begge er partall, kan man dele på 2 helt til man ikke kan dele lenger:
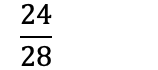
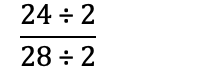
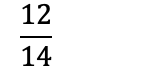
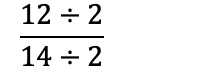
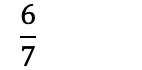
Om teller og nevner er oddetall, altså at de ikke kan deles på 2, må man prøve å dele på et oddetall:
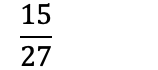
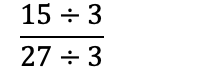
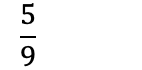
Å utvide brøk
Når vi utvider en brøk, ganger vi teller og nevner med det samme tallet. Dette gjør vi vanligvis når vi skal legge sammen to brøker, og trenger at begge brøkene har lik nevner.