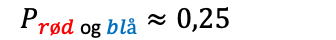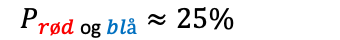Sannsynlighet handler om å måle sjansen for at en bestemt hendelse skal skje. Vi bruker som oftest brøk eller prosent for å uttrykke sannsynlighet.
Sannsynligheten for et utfall
Når vi skal regne ut sannsynligheten for et utfall, altså at noe skal skje, skriver vi regnestykket som ønsket utfall delt på mulige utfall. P her står for sannsynlighetstallet:
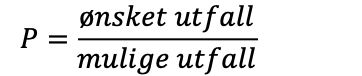
Eksempel
Regn ut sannsynligheten for å få krone når man kaster en mynt i luften?
Løsning:
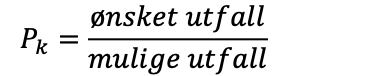
Ønsket utfall er 1, vi vil ha krone. Mulige utfall er 2, da vi kan få både krone og mynt:
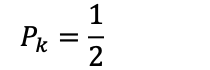
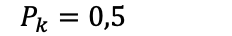
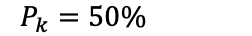
Sannsynligheten for å få krone når man kaster en mynt i luften er 50%
Komplementære hendelser
Hva er sannsynligheten for at noe IKKE skal skje?
Sannsynligheten for at noe ikke skal skje, er den resterende prosenten fra sannsynligheten for at det skal skje
Eksempel
Hva er sannsynligheten for å ikke få en hjerter når du trekker fra en kortstokk?
Løsning:
For å finne sannsynligheten for å ikke trekke hjerter, kan man først finne sannsynligheten for å faktisk trekke en hjerter
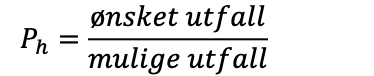
Det er 13 hjerter i en kortstokk, og 52 mulige kort man kan trekke:
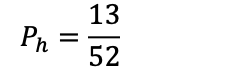

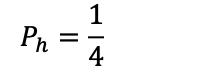
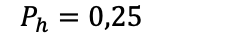
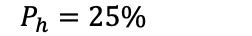
Det er altså 25% sjanse for å trekke hjerter. Det betyr at sjansen for å ikke trekke hjerter er 75%
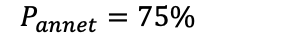
Addisjonssetningen
Addisjonssetningen brukes når vi kjenner sannsynligheten for flere ulike hendelser, og ønsker å finne sannsynligheten for at minst ett av hendelsene skal skje.
Man løser dette ved å legge sammen sannsynlighet for de ulike hendelsene
Eksempel 1
Hva er sannsynligheten for å trekke hjerter eller spar fra en kortstokk?
Løsning:
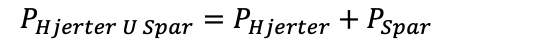
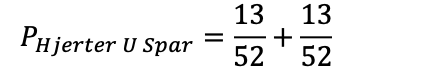
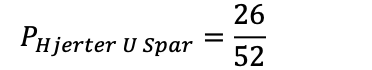
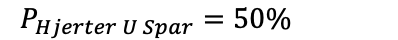
Det er 50% sannsynlighet for å trekke enten en hjerter eller en spar fra en kortstokk.
Eksempel 2
Hva er sannsynligheten for å trekke en kløver eller en treer fra en kortstokk?
Løsning:
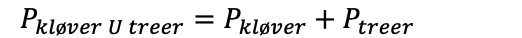
Her må man passe på. I likningen over regner vi med kløver3-kortet 2 ganger, ett blant kløverkortene og ett blant 3-kortene. Vi må derfor trekke fra dette kortet én gang:
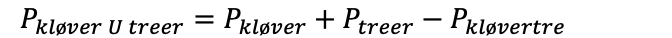
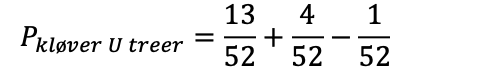
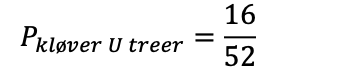
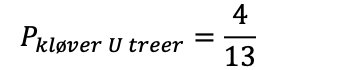
Sannsynligheten for å trekke en kløver eller en treer er 4 av 13, eller ca 31%
Uavhengige hendelser
Uavhengige hendelser er hendelser der utfallet av den ene hendelsen ikke påvirker utfallet av den andre. Med andre ord, sannsynligheten for at begge hendelsene inntreffer sammen er produktet av sannsynlighetene for at hver hendelse inntreffer alene.
Generell formel:
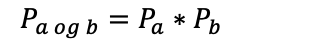
Eksempel
Du skal kaste to terninger. Hva er sannsynligheten for å få en toer på den ene, og et oddetall på den andre?
Løsning:
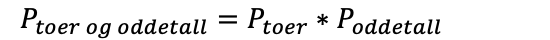
Det er seks tall på en terning, og det er én toer, så sannsynligheten for å få en toer blir 2 av 6. Det er tre oddetall på en terning, dermed 3 av 6 for oddetall:
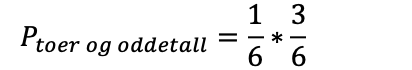
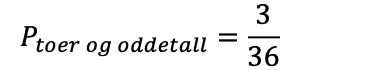
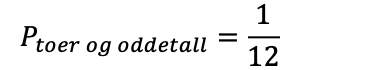
Avhengige hendelser
Avhengige hendelser er hendelser der utfallet av den ene hendelsen påvirker utfallet av den andre. Med andre ord, sannsynligheten for at den ene hendelsen inntreffer, avhenger av utfallet av den andre hendelsen.
Vi benytter generelt samme formel som ved uavhengige hendelser:
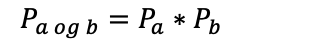
Eksempel
En boks inneholder 5 røde kuler og 4 blå kuler. Du trekker to kuler etter hverandre uten å legge dem tilbake i boksen. Hva er sannsynligheten for at den første kulen er rød og den andre kulen er blå?
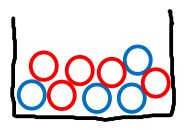
Løsning:
Vi ganger sammen sannsynligheten for hver av kulene, med formel:

Når vi skal trekke først en rød kule, er det totalt 9 kuler i boksen, og 5 røde kuler vi kan trekke:
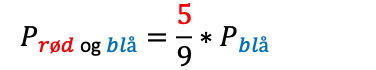
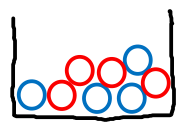
Etter at vi har trukket ut en rød kule, skal vi trekke en av de 4 blå kulene, men denne gangen er det én kule mindre i boksen, som betyr at det nå er 8 kuler å trekke blandt:
Dermed får vi:
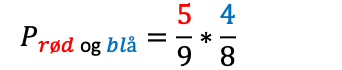
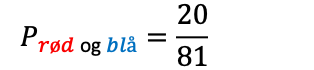
I prosent: